Exponential map
Motivation and general construction
(xournal_134)
Given a manifold $M$ we can think of a "procedure" that takes a point $p\in M$, a real number $t\in \mathbb{R}$ and a vector field $X$ on $M$ and returns a new point of $M$, working at this way:
1. we start at $p$ and move a little along $X_p$. That is, we compute $q_1=p+tX_p/10$. This is obviously not defined, but we take a blind eye. Also, we denote it by $q_1=p(Id+tX/10)$. This notation is justified because $X$ is, loosely speaking, an element of the Lie algebra of $\text{Dif}(M)$ so we can think of $Id+tX/10$ as an element of $\text{Dif}(M)$ near to $Id$.
2. we move a little from $q_1$ along the direction of $X_{q_1}$, that is, we compute $q_2=q_1+tX_{q_1}/10=q_1(Id+tX/10)$.
3. We finish after 10 steps.
Observe that, abusing of notation,
$$ q\approx q_{10}=q_9(Id+tX/10)=q_8(Id+tX/10)^2= $$ $$ =p(Id+tX/10)^{10} $$Of course, we have had better precision if we do this in more steps. In the limit (steps $\to \infty$) we would obtain the true output that we will denote by
$$ q=p \lim_{n\to \infty}(Id+tX/n)^{n} \equiv pe^{tX} $$and is nothing but the flow of $X$. (See also Lie algebra action. And Lie series.)
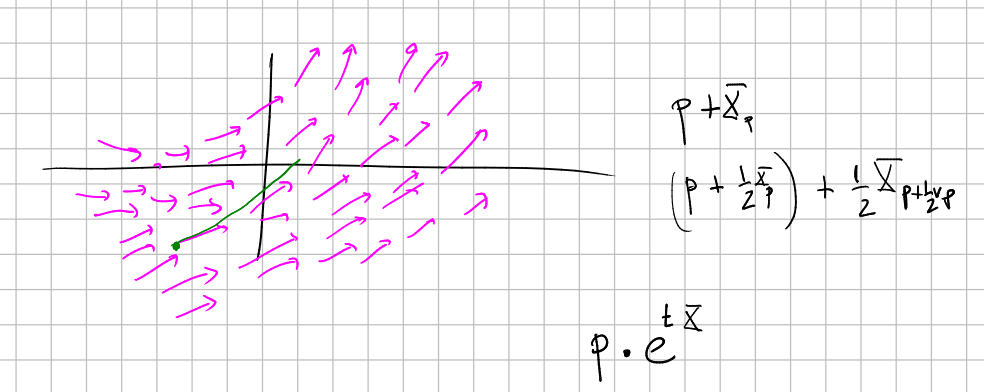
This is a very general construction, which allows you to find curves with a prescribed velocity.
Particular case: usual exponential function
What has to do with the usual exponential function and, moreover, with the number $e$? Suppose the manifold $M=\mathbb{R}$ and the vector field $X$ given in canonical coordinates by $X_x=x$.
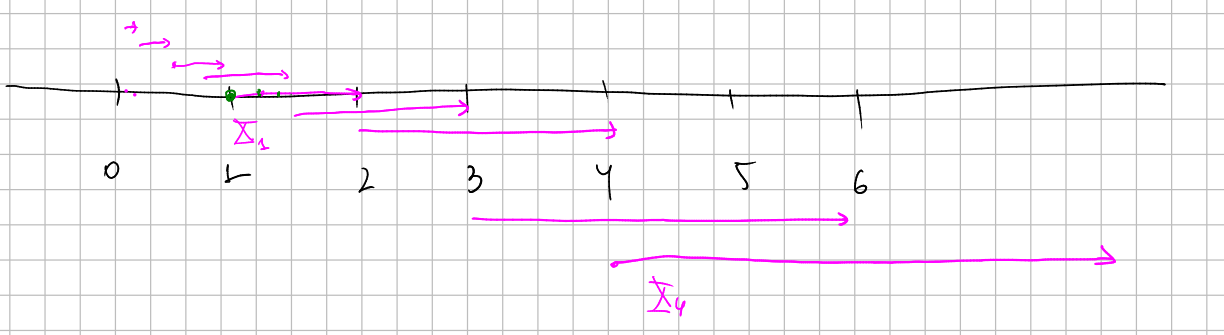
Then the number $e$ appears when we move from 1 a time 1 by means of that particular vector field.
That is, if you consider a curve $\alpha: \mathbb{R} \to \mathbb{R}$ such that $\alpha(0)=1$ and its velocity at $x$ is precisely $x$, then at time $t=1$ you will have arrived to position $e$.
Particular case: matrix exponential
This general construction can also be particularized to the case of matrix exponential. Suppose that the manifold is $M=GL(2,\mathbb{R})$ (it s valid for an arbitrary $GL(n)$, of course). So given any vector field $X\in \mathfrak{X}(GL(2,\mathbb{R}))$ we can define $e^{tX}$ as above.
But since in this case $M$ is a Lie group we can suppose that the chosen vector field $X$ is a left invariant vector field. Then it takes the form
$$ X_A=B\cdot A, $$being $A\in GL(2)$ (an invertible matrix) and $B\in T_{Id} GL(2)$ (an arbitrary matrix). When we compute $e^B$ what we are doing is to consider the corresponding left invariant vector field $X$ and move along its flow a time $t=1$ from the point $Id$.
Particular case: any Lie group
Consider a Lie group $G$, and an element $v$ in the Lie algebra $\mathfrak{g}$. Observe that, when we consider $G$ acting on itself, every vector $v\in T_{Id} G$ gives rise to a left invariant vector field $V\in \mathfrak{g}$ associated to $v$:
$$ V_g=d(L_g)_{Id}(v). $$Then, if we consider the flow $\phi_V$ of this vector field on $G$, we have a one-parameter subgroup of $\mbox{Diff}(G)$ (we are assuming that it is a complete vector field, which is something proven here.
With this set up, the exponential map is defined by
$$ exp(v)=\phi_V(1,Id) $$and is usually also denoted by $e^v$.
Since $G\subseteq \mbox{Diff}(G)$ we can wonder: is it, in fact, a one-parameter subgroup of $G$? Or in other words, does every diffeomorphism $\phi_V(t,-)$ correspond to left translation by an certain element $g_t \in G$?
The answer is yes. We can take $g_t=\phi_V(t,e)\in G$, and define $\tilde{\phi}(t,m)=m\cdot g_t$. But we can show that
$$ \phi_V=\tilde{\phi} $$because of the uniqueness of the flow, since:
- $\tilde{\phi}(0,m)=m=\phi_V(0,m)$
- $\tilde{\phi}(t,-)$ are integral curves of $V$:
Particular case: Riemannian manifolds
If we have a Riemannian manifold $(N,g)$ we have the exponential map for Riemannian manifolds:
$$ exp_p: T_pN \to N $$ $$ V\mapsto exp_p(V) $$How does it fit in this framework? If we consider the manifold $M=TN$ and the vector field $X\in \mathfrak{X}(TN)$ called the geodesic spray then we have, abusing of notation, $P=(p,V) \in TN$ and it turns out that
$$ P\cdot e^X=exp_p(V). $$Inverse relation with "differentiation"
It is important to note that $\phi_V(t,e)=e^{tv}$. But this is obvious from flow theorem for vector fields#Important property. Indeed
$$ e^{tv}=\phi_{tV}(1,e)=\phi_V(t,e). $$Therefore we have
$$ v=\frac{d}{dt}|_{t=0} e^{tv} $$expression that I like to call inverse relation between exponential and differentiation at the origin. In a sense, is like saying that exponentiation is like an "integration process" (see the picture of the section Motivation).
Local diffeomorphism of the Exponential Map
Consider the exponential map
$$ exp: \mathfrak{g} \mapsto G $$along with its differential at $0$:
$$ d (exp)_0: T_0 \mathfrak{g} \mapsto \mathfrak{g} $$The differential is the identity map, which implies, by the inverse function theorem, $exp$ acts as a diffeomorphism in a neighbourhood of $0\in \mathfrak{g}$ and $e\in G$. This neighbourhood is denoted as $U_e$. This ensures that the exponential map is always a local diffeomorphism at the origin of the Lie algebra. As a result, it sets up a local chart for a neighbourhood of the identity in the Lie group.
Global Behavior of the Exponential Map
It's essential to note that while the map acts as a diffeomorphism locally, its behavior can be different when viewed globally. Specifically:
- The exponential map may not be injective, which means distinct elements in the Lie algebra could end up mapping to the same element in the Lie group. This has to do with covering groups.
- The map might not be surjective. This implies there could be some elements in the Lie group that the exponential map cannot reach starting from the Lie algebra. Regarding the surjectivity we have two partial results:
Product Representation in $G$
According to Proposition 1.24 in @olver86, any element $g\in G$ can be expressed as a product of elements $g_i$ that belong to $U_e$. Formally, for any $g\in G$:
$$ g=g_1\cdot g_2\cdot \cdots = exp(v_1)\cdot exp(v_2)\cdot \cdots $$where each $v_i$ is an element of $\mathfrak{g}$.
Surjectivity of the Exponential Map
Proposition
For a compact connected Lie group $G$, the exponential map is surjective.
Proof
The proof is intricate and is provided in an external source. For a detailed understanding, refer to:
https://terrytao.wordpress.com/2011/06/25/two-small-facts-about-lie-groups/
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: